1.4 Statistical Approaches and Text Classification with N-grams

Approaching Language with Statistical Methods

When we think about language, we often think of it as a set of rules that govern how words can be combined to form valid sentences, but we just saw that there are countless exceptions that are hard to manage. What if we work the other way around, by using statistical methods to learn how words are distributed in a language from a corpus of texts?

Suppose we want to classify if an article talks about basketball. Consider these two approaches:

1. We manually build a set of rules (e.g. with grammars) with the help of a basketball expert to understand whether an article talks about basketball, such as the presence of some specific words like “basketball”, “basket”, “shot” or pieces of sentences like “play basketball”. This is the expert-system approach.

2. We group articles that we know to be about basketball and articles that aren’t about basketball, and let an algorithm derive the rules to discern between the two groups. This is the statistical (and machine learning) approach.

The expert system approach involves many trials and errors with different sets of rules. It can reach great precision but requires a lot of work. The statistical approach needs a dataset of high quality, but then it learns the rules automatically and can even work better than the expert system approach.

Text Classification with N-grams

Let’s see a brief example where we build a small statistical model that learns how to classify between texts that talk about basketball or football. We’ll do the following:

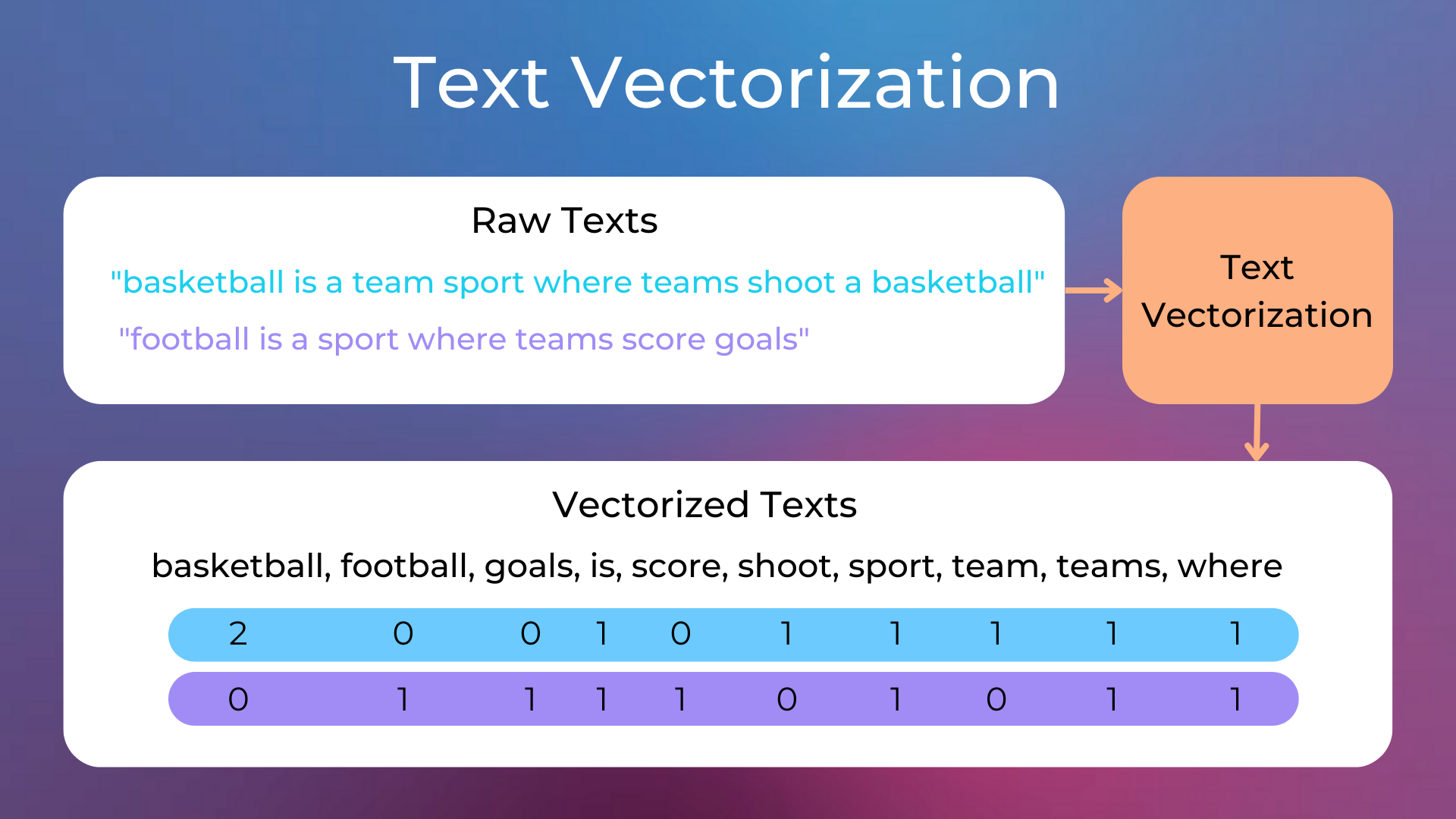
1. We vectorize some texts about basketball and football. By text vectorization we mean the process of converting text into a numerical vector that most machine learning models can understand (as models typically work with numbers, not words). This step can be done in different ways, but the easiest way is to count the number of occurrences of each word in the texts, which is what we’ll do in this example. We’ll see later in the course other ways of building more meaningful vectors.

2. We train a small logistic regression model on the vectorized texts.

3. We see the coefficients learned by the regression model, that is we see the importance of each word (learned by the model) in discerning whether the article is about basketball or football.

Text Vectorization

First, we import:

• The pandas library, to easily show tables with dataframes.

• The CountVectorizer class from sklearn, that we’ll use to vectorize texts by counting the occurrencies of each word.

• The LogisticRegression class from sklearn.

import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.linear_model import LogisticRegression

Then, we create a very small dataset of texts. In this example, for simplicity, we have only one text about basketball and one about football, but in real-world scenarios you want to have hundreds or thousands of examples to infer better rules.

We create a CountVectorizer object specifying the parameter ngram_range=(1,1), which means that it must consider only single words (i.e. unigrams) when counting their frequencies in the texts. Next, the vectorizer proceeds to count the words with the fit method.

texts = [
    "basketball is a team sport where teams shoot a basketball",
    "football is a sport where teams score goals"
]
labels = [1, 0] # 1 means basketball, 0 means football

# fit vectorizer on texts
vectorizer = CountVectorizer(ngram_range=(1, 1))
vectorizer.fit(texts) # build ngram dictionary

# vectorize texts into bag of words
ngrams = vectorizer.transform(texts)
ngrams.todense()

matrix([[2, 0, 0, 1, 0, 1, 1, 1, 1, 1],
        [0, 1, 1, 1, 1, 0, 1, 0, 1, 1]])

Once the vectorized is fit, it can be used to transform text into vectors with the transform method. The result is a scipy sparse matrix, which we can easiliy visualize by transforming it into a dense matrix with its todense method.

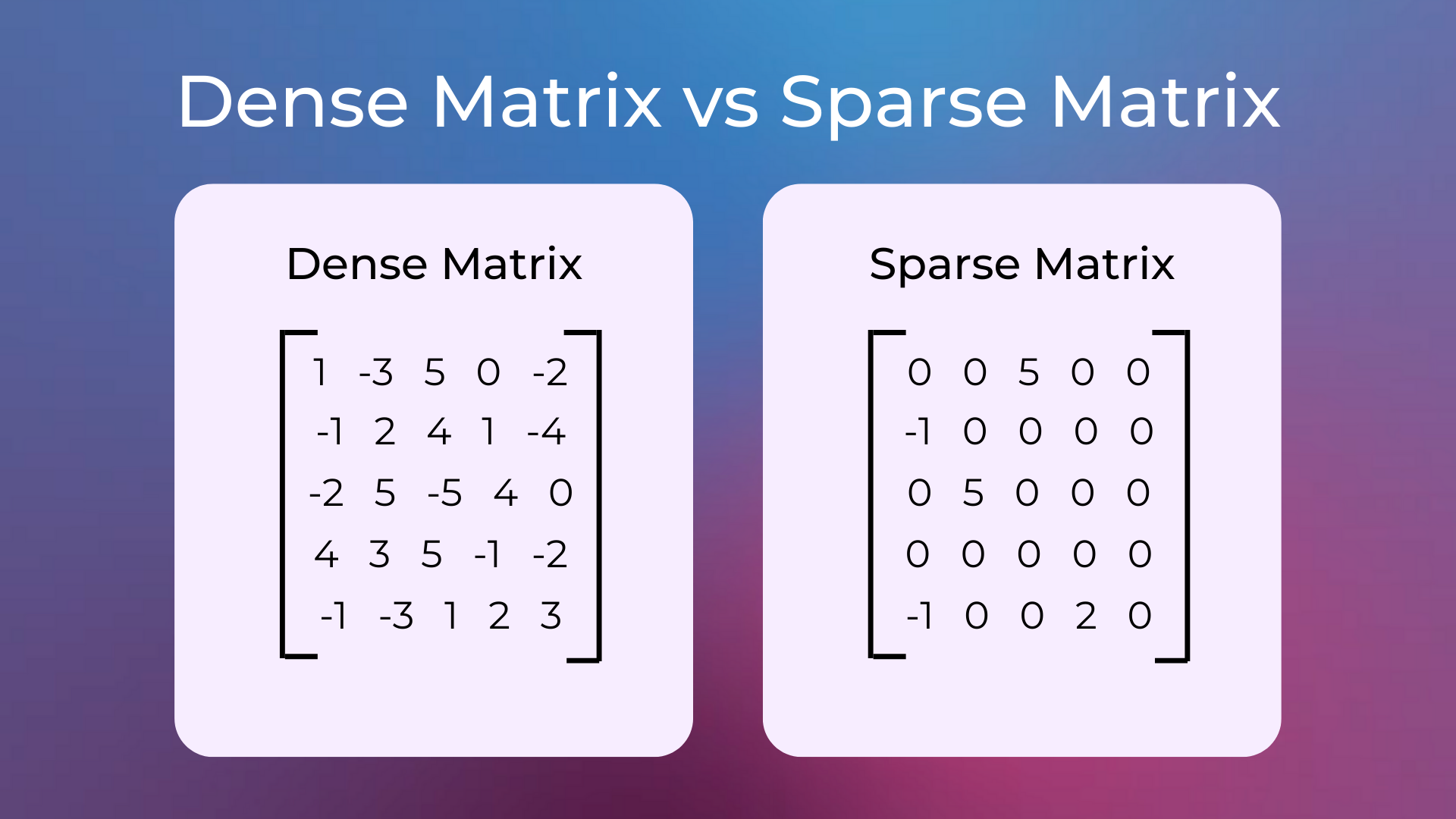
Sparse Matrix

A sparse matrix is a matrix in which most of the elements are zero. On the contrary, a dense matrix is a matrix where most of the elements are non-zero.

Since they have many elements with the same value, sparse matrices can be represented with different data structures than dense matrices, leading to less memory usage and more efficient matrix operations.

Sparse Matrix Formats

Sparse matrices can leverage different data structures, each one making specific matrix operations more efficient. Popular sparse matrix formats implemented in scipy are the Compressed Sparse Column matrix, the Compressed Sparse Row matrix, and the Row-based list of lists sparse matrix.

However, which word corresponds to which column? This relationship can be found within the vocabulary_ property of the vectorizer.

# show the vocabulary learned by the vectorizer
vectorizer.vocabulary_

{'basketball': 0,
 'is': 3,
 'team': 7,
 'sport': 6,
 'where': 9,
 'teams': 8,
 'shoot': 5,
 'football': 1,
 'score': 4,
 'goals': 2}

Using the info in the vocabulary of the vectorizer, we can obtain a pandas dataframe that shows how many times each word has been counted in each text.

# create a pandas dataframe that shows the unigrams in each text
keys_values_sorted = sorted(list(vectorizer.vocabulary_.items()), key=lambda t: t[1])
keys_sorted = list(zip(*keys_values_sorted))[0]
ngrams_matrix = ngrams.todense()
df = pd.DataFrame(ngrams_matrix, columns=keys_sorted)
df

	basketball	football	goals	is	score	shoot	sport	team	teams	where
0	2	0	0	1	0	1	1	1	1	1
1	0	1	1	1	1	0	1	0	1	1

A word is missing from the previous table… can you spot it? Do you know why it’s missing?

The missing word

From the table the word “a” is missing, which was present in both texts (e.g. “football is a sport where teams score goals”). We can investigate why it’s missing by reading carefully the documentation of the CountVectorizer class.

On the token_pattern parameter, we find out that the default tokenization uses a regexp that selects tokens of 2 or more alphanumeric characters (punctuation is completely ignored and always treated as a token separator). This is the reason we can’t find the “a” token in the output.

Model Training and Feature Weights

Next, we train a logistic regression model to distinguish between basketball and football texts and visualize the learned weights.

# train logistic regression on unigrams
model = LogisticRegression()
model.fit(ngrams, labels)

# show logistic regression weights
from_unigram_to_weight = dict(zip(keys_sorted, model.coef_[0]))
from_unigram_to_weight

{'basketball': 0.4946470025988935,
 'football': -0.24731844154410243,
 'goals': -0.24731844154410243,
 'is': 5.059755344317469e-06,
 'score': -0.24731844154410243,
 'shoot': 0.24732350129944675,
 'sport': 5.059755344317469e-06,
 'team': 0.24732350129944675,
 'teams': 5.059755344317469e-06,
 'where': 5.059755344317469e-06}

The word “basketball” has a positive score, while “football” and “goals” have negative scores. Irrelevant words like “is” have a score near zero. The more texts we have to train the model on, the better weights will be learned.

Bigrams

Let’s try using bigrams too. A bigram is made of two consecutive words, such as “score goals” in the sentence “football is a sport where teams score goals”. Bigrams may be necessary to grasp concepts expressed by multiple consecutive words like “New York” or “American football”. To do so, we simply create a CountVectorizer with ngram_range=(1,2), which means that both unigrams and bigrams will be counted.

# fit vectorizer on texts
vectorizer = CountVectorizer(ngram_range=(1, 2))
vectorizer.fit(texts) # build ngram dictionary

# vectorize texts into bag of words
ngrams = vectorizer.transform(texts)
ngrams.todense()

matrix([[2, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1],
        [0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1]])

Here are the extracted bigrams, such as “basketball is”, “team sport”, “sport where”, etc.

# show the vocabulary learned by the vectorizer
vectorizer.vocabulary_

{'basketball': 0,
 'is': 5,
 'team': 14,
 'sport': 12,
 'where': 19,
 'teams': 16,
 'shoot': 10,
 'basketball is': 1,
 'is team': 7,
 'team sport': 15,
 'sport where': 13,
 'where teams': 20,
 'teams shoot': 18,
 'shoot basketball': 11,
 'football': 2,
 'score': 8,
 'goals': 4,
 'football is': 3,
 'is sport': 6,
 'teams score': 17,
 'score goals': 9}

We can then again train a logistic regression model and visualize the weights of unigrams and bigrams.

# train logistic regression on ngrams
model = LogisticRegression()
model.fit(ngrams, labels)

# show logistic regression weights
keys_values_sorted = sorted(list(vectorizer.vocabulary_.items()), key=lambda t: t[1])
keys_sorted = list(zip(*keys_values_sorted))[0]
from_ngram_to_weight = dict(zip(keys_sorted, model.coef_[0]))
from_ngram_to_weight

{'basketball': 0.34694141625374514,
 'basketball is': 0.17347070812687257,
 'football': -0.173468461920609,
 'football is': -0.173468461920609,
 'goals': -0.173468461920609,
 'is': 2.2462062636252036e-06,
 'is sport': -0.173468461920609,
 'is team': 0.17347070812687257,
 'score': -0.173468461920609,
 'score goals': -0.173468461920609,
 'shoot': 0.17347070812687257,
 'shoot basketball': 0.17347070812687257,
 'sport': 2.2462062636252036e-06,
 'sport where': 2.2462062636252036e-06,
 'team': 0.17347070812687257,
 'team sport': 0.17347070812687257,
 'teams': 2.2462062636252036e-06,
 'teams score': -0.173468461920609,
 'teams shoot': 0.17347070812687257,
 'where': 2.2462062636252036e-06,
 'where teams': 2.2462062636252036e-06}

We can even build trigrams and so on. The generalization of this concept is called n-grams: unigrams are 1-grams, bigrams are 2-grams, trigrams are 3-grams, etc.

Note how in the previous example the words “team” and “teams” have different scores. The same could be said of verbs, like “eat”, “eats”, and “eating”. Ideally, we’d like to learn weights that are independent of singulars/plurals and verbal conjugations. We can do that with text normalization steps called stemming and lemmatization, which we’ll learn in the next lesson.

Bag of Words

The particular way of representing texts as a set of words is commonly called Bag of Words. Bag of Words is an easy way to represent texts with numbers that can be used as input to machine learning models.

However, as we’ll see later in the course, the bag of words representation has several disadvantages (such as not considering the order in which words appear in sentences) which will be addressed with more advanced models.

Code Exercises

Go to Notebook

Quiz

What is text vectorization?

1. The process of converting text into an unordered set of words.

2. The process of converting text into a numerical vector that most machine learning models can understand.

3. The process of converting text into vectors of words that are easier to use by machine learning models.

Answer

The correct answer is 2.

What does the ngram_range parameter of the CountVectorizer class specify?

1. The minimum and maximum number of n-grams to be extracted by the vectorizer.

2. The regular expression used for tokenization.

3. The lower and upper boundary of the range of n-values for different n-grams to be extracted.

Answer

The correct answer is 3.

What is a sparse matrix?

1. A matrix in which most of the elements are zero.

2. A matrix with few rows and columns.

3. A matrix with low rank.

Answer

The correct answer is 1.

What does the lowercase parameter of the CountVectorizer class specify?

1. Whether or not to convert all characters to lowercase before tokenizing.

2. Whether or not to convert all characters to lowercase after tokenizing.

3. To check if the input text is already lowercase.

Answer

The correct answer is 1.

What do the max_df and min_df parameters of the CountVectorizer class specify?

1. To ignore terms that have a document frequency respectively lower and higher than the two parameters.

2. To consider only terms that have a document frequency respectively higher and lower than the two parameters.

3. To ignore terms that have a document frequency respectively higher and lower than the two parameters.

Answer

The correct answer is 3.

What does the max_feature parameter of the CountVectorizer class specify?

1. To build a vocabulary that only considers the top max_features ordered by importance for predicting the label.

2. To build a vocabulary that only considers the top max_features ordered by term frequency across the corpus.

3. To build a vocabulary that only considers the bottom max_features ordered by term frequency across the corpus.

Answer

The correct answer is 2.

What is a bag of words representation?

1. A representation where text is represented as the set of its words, disregarding word order but considering grammar.

2. A representation where text is represented as the set of its words, disregarding grammar and even word order but keeping multiplicity.

3. A representation where text is represented as the ordered list of its words, disregarding grammar but keeping multiplicity.

Answer

The correct answer is 2.

Questions and Feedbacks

Have questions about this lesson? Would you like to exchange ideas? Or would you like to point out something that needs to be corrected? Join the NLPlanet Discord server and interact with the community! There’s a specific channel for this course called practical-nlp-nlplanet.